モンティ・ホール問題を知っていますか?
モンティ・ホール問題とは、ある条件下で行われる確率の問題のことを言います。
名前の由来はモンティ・ホールが司会を務める「Let’s make a deal」というアメリカのゲームショー番組からきています。
では、モンティ・ホール問題とはどのような問題なのか、例をあげて説明していきます。
例題「3つの箱に正解は1つ」
- とある3つの箱があります。
- 3つのうち、1つ箱を選んでもらいます。
- 1つの箱にだけ、金貨が入っています。
では、金貨の入った箱が当たる確率はいくらでしょうか?
この段階では、誰がどう考えても確率は1/3です。
では、ここで一手間加えます。
- とある3つの箱があります。
- 3つのうち、1つ箱を選んでもらいます。
- 1つの箱にだけ、金貨が入っています。
- ここで、答えを知っている出題者が残った2つの箱から空の箱を1つ開けます。
- このとき、残った1つの箱と交換できる権利が与えられます。
- 選んだ箱を交換しても良いし、そのままでも良いです。
では、このとき金貨の入った箱が当たる確率はいくらでしょうか?
これが「モンティ・ホール問題」です。
あなたは、金貨が当たる確率はいくらだと思いましたか?
では、計算してみましょう。
答えは 1/3?それとも 1/2?
まず、3つの箱をA、B、Cとします。
どの箱を選んでも、金貨が入っている確率は1/3です。
Aを選んだとして、次のステップへ進みます。
Aに金貨が入っていたと過程しましょう。
出題者は、残った2つの箱のうち、空の箱を開けます。
BとCは空の箱なので、開ける箱はどちらでも良いということになります。
Bを開けたとしましょう。
あなたが選んだ箱には金貨が入っているので、あなたはこの時点で「交換しない」という選択をとれば、当たりです。
Cを開けた場合も同じです。
このように、
「Aに金貨が入っていた場合、Bに金貨が入っていた場合、Cに金貨が入っていた場合」
「交換した場合、交換しなかった場合」
を場合分けしてみると、以下のようになります。
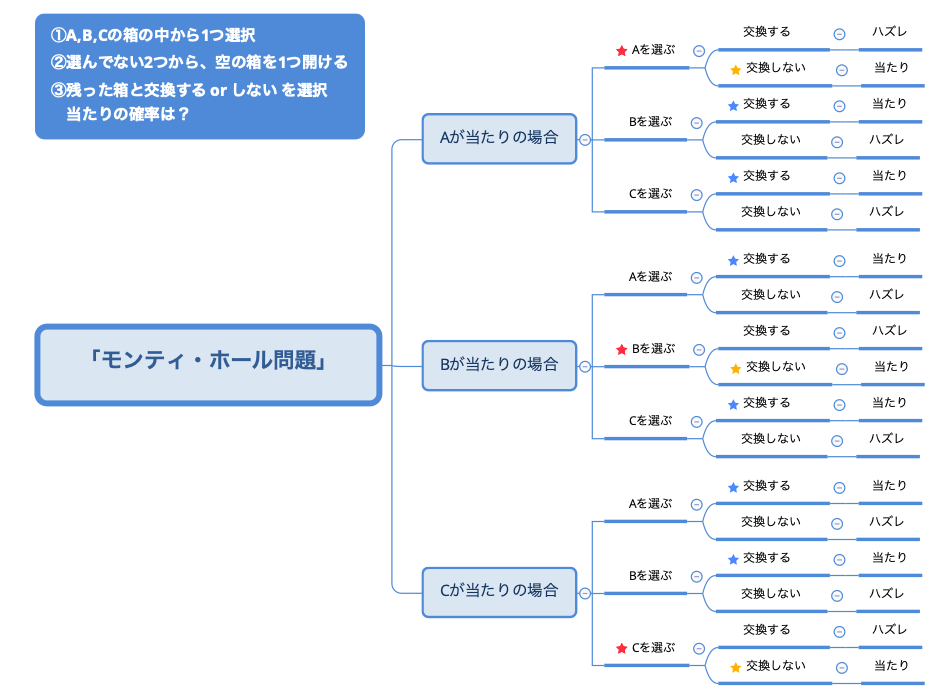
黄色の★が「交換しないで当たる事象」、青色の★が「交換して当たる事象」です。
すると、「交換する場合」と「交換しない場合」で確率が異なることがわかります。
交換しなかった場合、最初と同じ1/3。
一方交換した場合、当たる確率は2/3になります。
なぜこのようなことが起こるのでしょうか?
ポイントとなるのは、出題者が必ず「空の箱を開ける」という点です。
つまり、自分がもし空の箱を引いた場合、必ず残った箱には金貨が入っていることになります。
これにより、単純に「1/2」と考えてしまう錯覚に陥るのです。
主観がもたらす確率のズレ
この問題から言えることは「自分が咄嗟に出した主観的な確率と、実際の確率が異なっている」ということです。
実は、この問題を京都大学出身者出しても、ほとんどの人が最初に「どちらにしても変わらない」と思ったそうです。
モンティ・ホール問題は「私たちの主観は意外とズレていることもあるから、物事を判断するときは冷静に分析する必要がある」ということを教えてくれている問題とも捉えることができるでしょう。
私たちは、自分の出した答えは一度疑ってみる必要があるかもしれません。
冷静になって考えると、自分の意見なんて的外れな場合も多いのです。
